Harnessing the Power of KAN: A Leap in Neural Network Architecture

Do Data Scientists need to replace all MLP to KAN? Let's explore it.

The world of machine learning is abuzz with the introduction of a novel neural network structure known as KAN, or Kolmogorov-Arnold Networks. This groundbreaking architecture was first introduced in a preprint on arXiv on April 30, 2024, marking a significant departure from traditional Multi-Layer Perceptrons (MLPs).

What is KAN?

KAN is designed based on the Kolmogorov-Arnold representation theorem, which allows for the direct learning of non-linear activation functions. This design choice leads to a more parameter-efficient network with higher interpretability of learning outcomes. Unlike MLPs that use fixed activation functions, KANs adaptively learn activation functions, which can be visualized as the shape of the original function relationships being directly reflected in the activation functions. The machine learning community has recently shown a keen interest in the KAN, which offers an intriguing option compared to the conventional Multi-Layer Perceptron (MLP). Considering MLPs are crucial elements in various models, such as Transformers that drive current large language model (LLM) applications, the rise of KAN could herald significant shifts in the domain.

The Mathematical Foundation The Kolmogorov-Arnold representation theorem posits that any continuous multivariate function can be represented as a composition of a finite number of continuous univariate functions. This theorem lays the foundation for KAN’s two-layer nested structure, which simplifies the complex interplay of functions into a more manageable form.

Kolmogorov–Arnold representation theorem (or superposition theorem) states that every multivariate continuous function f

can be represented as a superposition of the two-argument addition of continuous functions of one variable where

\(f(x) = f(x_1,...,x_n)=\sum_{q=1}^{2n+1}\Phi_q(\sum_{p=1}^n \phi_{q,p}(x_p))\)

\(\text{s.t.} \hspace{1cm} \phi_{q,p} : [0, 1] \rightarrow \mathbb{R} \hspace{1cm} \Phi_q: \mathbb{R} \rightarrow \mathbb{R}\)

see example here: analysis - Are there any simple examples of Kolmogorov-Arnold representation? - Mathematics Stack Exchange.

KAN’s Structure and Learning Mechanism KANs utilize a two-layer structure that can be extended to construct more complex models. This is achieved by stacking more than two layers, each referred to as a Kolmogorov-Arnold layer. The computation within the network is straightforward, where the output of the previous layer serves as the input to the functions in the subsequent layer.

\({f(x)={\bf \Phi}_{\rm out}\circ{\bf \Phi}_{\rm in}\circ {\bf x} }\)

\({\begin{split}{\bf \Phi}_{\rm in}= \begin{pmatrix} \phi_{1,1}(\cdot) & \cdots & \phi_{1,n}(\cdot) \\ \vdots & & \vdots \\ \phi_{2n+1,1}(\cdot) & \cdots & \phi_{2n+1,n}(\cdot) \end{pmatrix},\quad {\bf \Phi}_{\rm out}=\begin{pmatrix} \Phi_1(\cdot) & \cdots & \Phi_{2n+1}(\cdot)\end{pmatrix}\end{split} }\)

The two-layer structure mentioned earlier is limited in its expressive power, especially with the functions available for implementation. Therefore, we consider constructing more complex models by stacking more than two layers.

In doing so, the matrix representation mentioned earlier is useful, and the model can be expressed as follows:

\({{\rm KAN}({\bf x})={\bf \Phi}_{L-1}\circ\cdots \circ{\bf \Phi}_1\circ{\bf \Phi}_0\circ {\bf x} }\)

Here, the generalized layer is referred to as the Kolmogorov-Arnold layer.

\({\begin{split}{\bf \Phi}= \begin{pmatrix} \phi_{1,1}(\cdot) & \cdots & \phi_{1,n_{\rm in}}(\cdot) \\ \vdots & & \vdots \\ \phi_{n_{\rm out},1}(\cdot) & \cdots & \phi_{n_{\rm out},n_{\rm in}}(\cdot) \end{pmatrix}\end{split} }\)

While individual functions will be modeled as described later, the overall computation of the network is a simple mechanism that proceeds by inputting the output of the previous layer into the function, based on the positional relationship of the matrix product.

Modeling Individual Activation Functions One of the proposed methods for modeling individual activation functions within KANs is through B-spline curves. These curves are expressed as a sum of bell-shaped polynomials centered around control points. While B-splines offer flexibility in representing various curve shapes, they are limited by the finite number of control points. To address this, the implementation dynamically updates the position of control points based on the input range, ensuring that the new control points’ coefficients best approximate the previous shape using the least squares method.

x = evaluated point
prev_spline_coeffs = spline_coeffs
prev_spline_bases = b_spline(x, grid)
prev_spline = sum(prev_spline_coeffs*prev_spline_bases)
grid = new_grid
new_spline_bases = b_spline(x, new_grid)
spline_coeffs = least_square_fit(new_spline_bases, prev_spline)

MLP vs KAN

Empirical Evidence of KAN’s Capabilities

The prowess of KANs is not merely theoretical. Empirical evidence from the original documentation reveals their robustness across a spectrum of tasks. KANs have been applied to classification tasks, symbolic regression, solving partial differential equations, and even unsupervised learning scenarios. In each instance, KANs have demonstrated an impressive combination of flexibility and expressive power, often outperforming traditional neural networks with fewer layers and parameters.

When considering the computational aspects of KAN and MLP, one might wonder if they are simply variations of neural networks with different nonlinear approaches. However, the significance lies deeper.

Computational Aspects of KAN vs. MLP

At first glance, one might consider KAN and Multilayer Perceptron (MLP) to be mere variations of neural networks with different nonlinear approaches. However, the distinction between them is profound. KANs offer a solution to the notorious challenge of high-dimensional function approximation that plagues many neural network models.

KAN allows us to escape the curse of dimensionality in function fitting.

\(a = \sum_{p=1}^n \phi_{q,p}(x_p) \hspace{1cm} a = f(wx + b)\)

In Multilayer Perceptrons (MLPs), the activation function is influenced by the collective inputs, while in Kernelized Architecture Networks (KANs), it is determined by just one input. This key difference allows for the application of diverse function approximation methods without being limited by the curse of dimensionality.

B-Splines demonstrate a localized influence confined to specific segments.

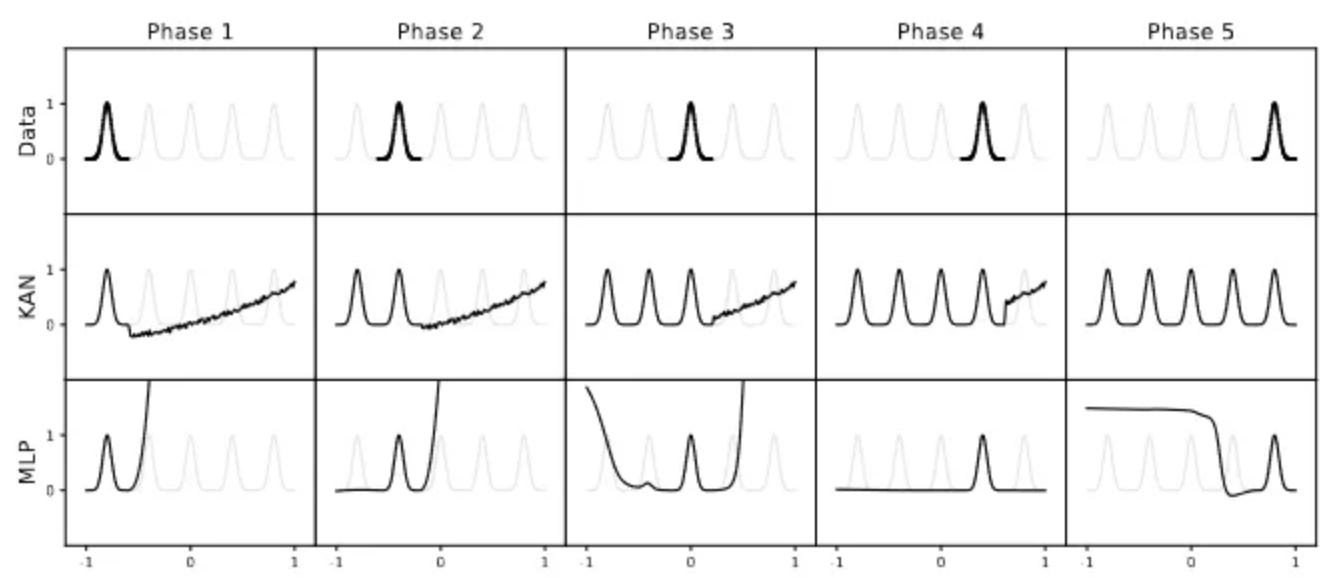
KAN mitigates the issue of catastrophic forgetting.

As illustrated in the research, when tackling a simple continual learning challenge that entails a one-dimensional regression task characterized by five Gaussian peaks, Kernelized Architecture Networks (KANs) demonstrate a robust ability to prevent catastrophic forgetting. In contrast, Multilayer Perceptrons (MLPs) suffer from significant catastrophic forgetting under the same conditions.

The Future of KAN

In conclusion, the emergence of KANs represents a significant leap in neural network architecture. With their ability to learn activation functions directly and their strong mathematical foundation, KANs are poised to accelerate the development of machine learning and open up new possibilities for researchers and practitioners alike.

The following perspective is intriguing scope for further research and application to real world data: inductive bias of KAN vs MLP and proven success of KAN for winning solution in Kaggle community.

Implimentation

Pytorch implementation is provided with following github repository:

1. Blealtan/efficient-kan: An efficient pure-PyTorch implementation of Kolmogorov-Arnold Network (KAN). (github.com)

2. IvanDrokin/torch-conv-kan: This project is dedicated to the implementation and research of Kolmogorov-Arnold convolutional networks. The repository includes implementations of 1D, 2D, and 3D convolutions with different kernels, ResNet-like and DenseNet-like models, training code based on accelerate/PyTorch, as well as scripts for experiments with CIFAR-10 and Tiny ImageNet. (github.com)

References & Links

KAN: Kolmogorov–Arnold Networks (arxiv.org)

Linkedin profile: www.linkedin.com/in/takehiro-ohashi-b54101174